How to Generate Random Colors Programmatically

Creating random colors is actually more difficult than it seems. The randomness itself is easy, but aesthetically pleasing randomness is more difficult. For a little project at work I needed to automatically generate multiple background colors with the following properties:

• Text over the colored background should be easily readable
• Colors should be very distinct
• The number of required colors is not initially known

Naïve Approach

The first and simplest approach is to create random colors by simply using a random number between [0, 256[ for the R, G, B values. I have created a little Ruby script to generate sample HTML code:

# generates HTML code for 26 background colors given R, G, B values.
def gen_html
  ('A'..'Z').each do |c|
    r, g, b = yield
    printf "<span style=\"background-color:#%02x%02x%02x; padding:5px; -moz-border-radius:3px; -webkit-border-radius:3px;\">#{c}</span> ", r, g, b
  end
end

naive approach: generate purely random colors

gen_html { [rand(256), rand(256), rand(256)] }

The generated output looks like this:

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

As you can see this is quite suboptimal. Some letters are hard to read because the background is too dark (B, Q, S), other colors look very similar (F, R).

Using HSV Color Space

Let’s fix the too dark / too bright problem first. A convenient way to do this is to not use the RGB color space, but HSV (Hue, Saturation, Value). Here you get equally bright and colorful colors by using a fixed value for saturation and value, and just modifying the hue:

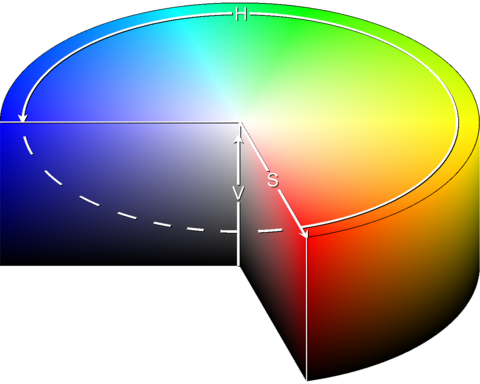
Based on the description provided by the wikipedia article on conversion from HSV to RGB I have implemented a converter:

# HSV values in [0..1[
# returns [r, g, b] values from 0 to 255
def hsv_to_rgb(h, s, v)
  h_i = (h*6).to_i
  f = h*6 - h_i
  p = v * (1 - s)
  q = v * (1 - f*s)
  t = v * (1 - (1 - f) * s)
  r, g, b = v, t, p if h_i==0
  r, g, b = q, v, p if h_i==1
  r, g, b = p, v, t if h_i==2
  r, g, b = p, q, v if h_i==3
  r, g, b = t, p, v if h_i==4
  r, g, b = v, p, q if h_i==5
  [(r*256).to_i, (g*256).to_i, (b*256).to_i]
end

Using the generator and fixed values for saturation and value:

# using HSV with variable hue
gen_html { hsv_to_rgb(rand, 0.5, 0.95) }

returns something like this:

Much better. The text is easily readable, and all colors have a similar brightness. Unfortunately, since we have limited us to less colors now, the difference between the randomly generated colors is even less than in the first approach.

Golden Ratio

Using just rand() to choose different values for hue does not lead to a good use of the whole color spectrum, it simply is too random.

Here I have generated 2, 4, 8, 16, and 32 random values and printed them all on a scale. Its easy to see that some values are very tightly packed together, which we do not want.

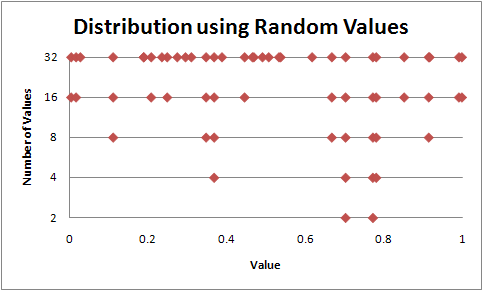
Lo and behold, some mathematician has discovered the Golden Ratio more than 2400 years ago. It has lots of interesting properties, but for us only one is interesting:

[…] Furthermore, it is a property of the golden ratio, Φ, that each subsequent hash value divides the interval into which it falls according to the golden ratio!

– Bruno R. Preiss, P.Eng.

Using the golden ratio as the spacing, the generated values look like this:

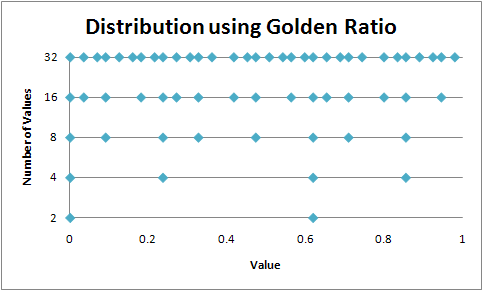
Much better! The values are very evenly distributed, regardless how many values are used. Also, the algorithm for this is extremely simple. Just add 1/Φ and modulo 1 for each subsequent color.

# use golden ratio
golden_ratio_conjugate = 0.618033988749895
h = rand # use random start value
gen_html {
  h += golden_ratio_conjugate
  h %= 1
  hsv_to_rgb(h, 0.5, 0.95)
}

The final result:

You can see that the first few values are very different, and the difference decreases as more colors are added (Z and E are already quite similar). Anyways, this is good enough for me.

And because it is so beautiful, here are some more colors

s=0.99, v=0.99

s=0.25, h=0.8

s=0.3, v=0.99

Have fun! Martin