In part 1 I have discussed Hopscotch and Robin Hood Hashing table. Since then I have implemented several hashmap variants that combine some tricks from these two variants, and have some interesting results to share. Here are the variations that I have implemented:
Robin Hood with Infobyte
Robin Hood Hashing uses the hash value to calculate the position to place it, than does linear probing until it finds an empty spot to place it. While doing so it swaps out entries that have a lesser distance to its original bucket. This minimizes the maximum time a lookup takes. For a lookup, it is only necessary to lineary probe until the distance to the original bucket is larger than the current element’s distance.
In this “Infobyte” implementation variant, instead of storing the full 64 bit hash value I directly store the distance to the original bucket in a byte. One bit of this byte is used to mark the bucket as taken or empty. The bit layout is defined like this:

When storing four elements a, b, c, d, where a, b map to hash position 1 and c, d to hash position 2, this is how they would be stored:
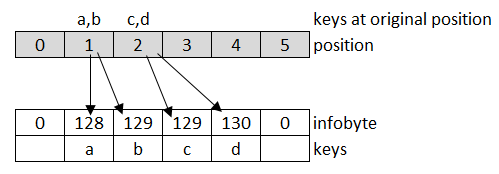
The advantage is that I have just 1 byte instead of 8 overhead, and linear probing is faster because I need only comparison operation on a single byte instead of calculating offsets with the hash. A byte is more than enough for the offset, since on average the distance to the the original bucket is very small. Here is the full code for lookup:
const Val* find(const Key& key) const {
size_t idx = _hash(key) & _mask;
// IS_BUCKET_TAKEN_MASK is 128 (1000 0000 in binary)
std::uint8_t info = Traits::IS_BUCKET_TAKEN_MASK;
while (info < _info[idx]) {
++idx;
++info;
}
// check while info matches with the source idx
while (info == _info[idx]) {
if (key == _keys[idx]) {
return _vals + idx;
}
++idx;
++info;
}
// nothing found!
return nullptr;
}
This search is very simple and straightforward, and fast.
Robin Hood with Infobits & Hashbits
Using a full byte for the offset (actually 7 bit) is fairly large. This would allow an offset of 127, which would lead to a very long and slow linear probing. My idea then is to limit the offset to a much lower maximum number. The remaining bits of the byte can be used to store a few bits from the hash, so that we can use these few bits to reduce the number of key comparisons. Also these hashbits could be used when resizing the hashmap so we would not have to rehash all elements each time we resize. After some tuning, this is the bit layout I am using for this variant:

The much smaller offset means that when inserting an element and the maximum offset is reached, I have to resize the hashmap. This is intentional, since very large offset would lead to slow searches. This way this hashing variant is more similar to Hopscotch. Here is the full code to lookup an element with this byte:
const Val* find(const Key& key) const {
auto h = _hash(key);
// create info field: offset is bucket is taken, offset is 0, with hash info.
std::uint8_t info = Traits::IS_BUCKET_TAKEN_MASK | ((h >> _level_shift) & Traits::HASH_MASK);
// calculate array position
size_t idx = h & _mask;
// find info field
while (info < _info[idx]) {
++idx;
info += Traits::OFFSET_INC;
}
// check while it seems we have the correct element
while (info == _info[idx]) {
if (key == _keys[idx]) {
return _vals + idx;
}
++idx;
info += Traits::OFFSET_INC;
}
return nullptr;
}
The find code is almost exactly like in the pure Infobyte variant, except that I am or’ing 3 hash bits into the info byte, and instead of ++info I am using info += Traits::OFFSET_INC where OFFSET_INC is 16 (1000b).
Robin Hood with Infobyte & Fastforward
In the first variant of Robin Hood Hashing finding an element will be slow as the hashmap gets full, because a lot of elements need to be skipped before finding the full one. Robin hood hashing has the property that it always keeps elements that belong to the same bucket together. The infobyte introduced in the first variant basically acts as a backpointer to the bucket that element originally belongs to, and it is possible to introduce another byte that is stored at the original bucket, that acts as a forward pointer to where the first element is stored for this original bucket.
Using the above example where (a, b) maps to 1 and (c, d) to 2 fastforward byte looks like this:
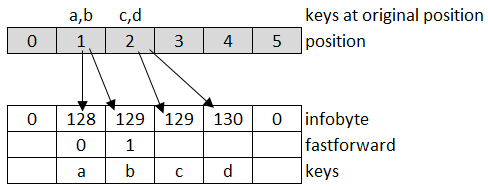
When looking up element c, the fastforward byte can be used to skip one element, so the while (info < _info[idx]) { ... } can be replaced with the skip operation. Here is the code:
const Val* find(const Key& key) const {
size_t idx = _hash(key) & _mask;
const auto ff = _info[idx].fastforward;
std::uint8_t info = Traits::IS_BUCKET_TAKEN_MASK | ff;
idx += ff;
// check while info matches with the source idx
while (info == _info[idx].info) {
if (key == _keys[idx]) {
return _vals + idx;
}
++idx;
++info;
}
// nothing found!
return nullptr;
}
I am using a struct that contains two bytes: info field, and fastforward. Now I have two bytes overhead for each entry, but can quickly skip lots of buckets which should be especially useful when the hashmap is very full.
Hopscotch
Hopscotch can be seen as quite similar to the robin hood hashing with fastforward, except that it replaces the info and fastforward byte with a bitmask. With some tuning I am now using a 16 bit field, where 1 bit is used to define if the current bucket is full, and the other bits define which offsets to the current bucket are taken.
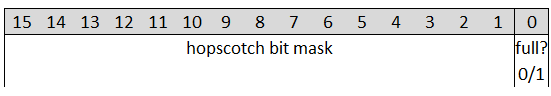
If the first bit is set, the current bucket is taken; but not nessarily by the bucket from this hop bitfield. This bit is not strictly necessary because that information is also encoded in the different hop tables, but it speeds up insertion code. With 16 bits available, this limits the hop bits to 15 though. As with “Robin Hood Hashing with Infobits & Hashbits”, when the hop bits are full, the hashmap has to be resized.
Benchmark Results
I’m leaving the most important information for part 3: how do all these variant perform? What’s best?